http://www.imatest.com/docs/colormatrix.html
Introduction
Multicharts can calculate a color correction matrix that can be applied to images to achieve optimum color balance, as defined by minimizing a color error parameter on the test chart of choice. (The default is the mean of (Delta-E 94)2 for all patches where L*>10 and L*<95.)>
Some of the background for the calculation can be found in Color Correction Matrix for Digital Still and Video Imaging Systems by Stephen Wolf, though the Imatest calculation differs in many respects: there is no issue with outliers and optimization is performed using one of the standard color difference metrics.
The color correction matrix is initially included only in Multicharts.

The Math
The matrix
Color images are stored in m x n x 3 arrays (m rows (height) x n columns (width) x 3 colors). For the sake of simplicity, we transform the color image to a k x 3 array, where k = m x n. An Original (uncorrected) array O can be represented as
| O_R1 O_G1 O_B1 | O = | O_R2 O_G2 O_B2 | | ... |
| ... |
| O_Rk O_Gk O_Bk |
where O_Ri, O_Gi, and O_Bi represent the normalized R, G, and B levels of pixel i. The transformed (corrected) array is calledP, where
P = O A (case 1: A is a 3x3 matrix) — or —
P = [O 1] A (case 2: A is a 4x3 matrix; the added column of 1s provides a dc-offset)
A is the 3x3 or 4x3 color correction matrix. For the 3x3 matrix (case 1),
| P_R1 P_G1 P_B1 | | O_R1 O_G1 O_B1 | P = | P_R2 P_G2 P_B2 | = | O_R2 O_G2 O_B2 | | A11 A12 A13 | | ... | | ... | X | A21 A22 A23 |
| ... | | ... | | A31 A32 A33 |
| P_Rk P_Gk P_Bk | | O_Rk O_Gk O_Bk |
X denotes matrix multiplication. In this case, for row m,
P_Rm = O_Rm*A11 + O_Gm*A21 + O_Bm*A31 (* denotes multiplication.)
P_Gm = O_Rm*A12 + O_Gm*A22 + O_Bm*A32
P_Bm = O_Rm*A13 + O_Gm*A23 + O_Bm*A33
For the 4x3 matrix (case 2), a column of 1s is added to provide a dc-offset,
| P_R1 P_G1 P_B1 | | O_R1 O_G1 O_B1 1 | | A11 A12 A13 | P = | P_R2 P_G2 P_B2 | = | O_R2 O_G2 O_B2 1 | | A21 A22 A23 | | ... | | ... | X | A31 A32 A33 |
| ... | | ... | | A41 A42 A43 |
| P_Rk P_Gk P_Bk | | O_Rk O_Gk O_Bk 1 |
In this case, for row m,
P_Rm = O_Rm*A11 + O_Gm*A21 + O_Bm*A31 + A41
P_Gm = O_Rm*A12 + O_Gm*A22 + O_Bm*A32 + A42
P_Bm = O_Rm*A13 + O_Gm*A23 + O_Bm*A33 + A43
The goal of the calculation is to minimize the difference (the mean square error metric) between P and the reference array (the ideal chart values) R. The initial values of A (the starting point for optimization) for the 3x3 and 4x3 cases, are
| k_R 0 0 | | k_R 0 0 | A(3x3) = | 0 k_G 0 | ; A(4x3) = | 0 k_G 0 | | 0 0 k_B | | 0 0 k_B |
| 0 0 0 |
where
k_R = mean(R_Ri ; all i) ⁄ mean(O_Ri ; all i) for reference array R and original array O
k_G = mean(R_Gi ; all i) ⁄ mean(O_Gi ; all i)
k_B = mean(R_Bi ; all i) ⁄ mean(O_Bi ; all i)
These starting values are closer to the final values (have less mean square error) than the identity matrix (k_R = k_G = k_B = 1). They tend to converge slightly better.
Linearization
Although most digital image sensors are linear up to the point where they saturate, image files are highly nonlinear— they are designed for display at a specified gamma ( γ ), where display luminance = pixel levelγ. Gamma = 2.2 for the most commonly used color spaces (sRGB, Adobe RGB (1998) and Wide Gamut RGB (WGRGB)), although some well-known color spaces are designed for display at gamma = 1.8 (ProPhoto, Apply, ColorMatch; all RGB).
When cameras encode images (a part of the RAW conversion process), they apply a gamma that is the approximate inverse of the display gamma. Perhaps we should say very approximate: it may vary considerably from 1/γ, and it often includes a tonal response curve "shoulder" (an area of reduced contrast) to minimize highlight burnout. The shoulder makes the response more "film-like," improving pictorial quality in most instances.
If the input image is gamma-encoded you may wish to linearize the image prior to applying the correction matrix. Imatest has several linearization options.
Optimization steps
- (Optionally) linearize the input image. If Color space gamma linearization is selected, OL = Oγ.
- Call the optimizer, which
- calculates a (temporary) corrected image TL = OL A.
- (Optionally) removes the linearization: T = TL(1/γ)
- Finds the mean of squares of errors between T and the reference (ideal) array R. The error is one of the standard error measurements: ΔE*ab, ΔC*ab, ΔE94, ΔE94, ΔECMC, ΔCCMC, ΔE00, or ΔC00, described here. ΔE94 is the recommended default. Although the CIEDE2000 color error metrics (ΔE00, ...) are more accurate, they contain small discontinuities that can affect optimization, and hence they should be used with caution. SeeSharma for details. The ΔC errors are similar to ΔE with luminance (L*) omitted.
- Adjusts A until a minimum value of the sum of squares of the errors is found, using nonlinear optimization.
- Report the final value of A.
In applying A (generally outside of Imatest), a similar linearization should be used. A may be applied during the RAW conversion process, prior to the application of the gamma + tonal response curve.
There is no guarantee that A is a global minimum. Its final value depends to some extent on its starting value.
The Color correction matrix in Multicharts
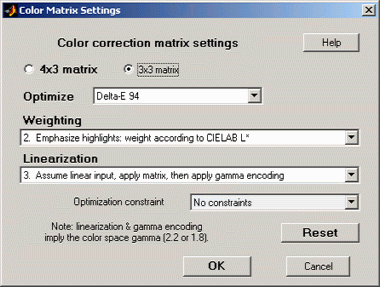
Options: Color matrix calculation options can be set by clickingSettings, Color matrix in the Multicharts window. This brings up the dialog box shown on the right. The options are
- 4x3 or 3x3 matrix: Color correction matrix size. The 4x3 matrix (the default) includes a dc-offset (constant) term. It may be slightly more accurate, but it takes more computation time.
- Optimize: Select the color error parameter whose mean of squares over patches with L*>10 (nearly black for <10;>95) is to be minimized. Choices include ΔE ab, ΔC ab, ΔE 94, ΔE 94, ΔE CMC, ΔC CMC, ΔE 00, and ΔC 00, described here. ΔE 94 is the default value, recommended because it gives less weight to chroma differences between highly chromatic (saturated; large a*2 + b*2 ) colors, which is closer to the eye's perception than ΔE ab (the standard ΔE value: the geometrical distance between colors in L*a*b* space).
- Weighting: Set the weighting of the patches for optimization. Choices:
- 1. Equal weighting [default] Patches are equally weighted. May not be the optimum setting because highlight colors may be more visually prominent than shadow colors.
- 2. Emphasize highlights: weight according to CIELAB L* Give more weight to visually-prominent hightlight patches.
- 3. Strongly emphasize highlights: weight according to L*^2.
- Linearization: Choose the method of linearizing the image (or leave it unchanged). For linearization or gamma encoding, the value of gamma ( γ ) for the selected color space (sRGB, Adobe RGB, etc.) is used. The equation for linearization isOL = O1/γ. The equation for gamma application O = OLγ.
- 1. Linearize input, apply matrix, then apply gamma encoding. Usually the best choice for images encoded in a standard color space.
- 2. No linearization: apply matrix to input pixels. May not be the best choice for gamma-encoded images, but useful for experimentation and for images that start and remain linear.
- 3. Assume linear input, apply matrix, then apply gamma encoding. A good choice for images that are not gamma-encoded, but need to be converted into a color space. Color space gamma is not applied in converting the input RGB image to L*a*b*.
- 4. Assume linear input & output (gamma = 1 throughout). No linearization or gamma encoding. Color space gamma is not applied in converting between RGB and L*a*b* spaces.
- Optimization constraint
- No constraints. This is the default and should only be changed with good reason.
- Rows sum to 1.
- Columns sum to 1.

To calculate the color correction matrix, read the image into Multicharts, then press the Correction matrix button, shown on the right. The display will change, as shown below. The improvement for this image, which is quite good to begin with, is undramatic.
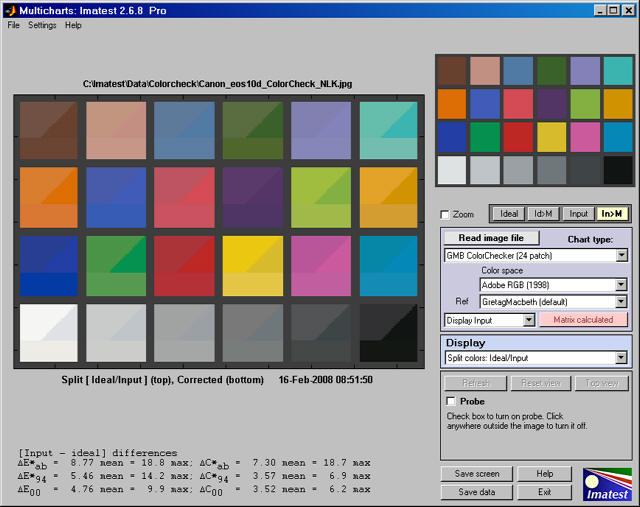
Split view, showing reference, input, and corrected patch colors
The image now shows the corrected colors on the bottom of each patch. The ideal (reference) color remains in the upper-left and the input (original) color remains in the upper right.
The Correction matrix button changes to Matrix calculated, highlighted with a pink background. The correction matrix cannot be recalculated until an image property changes (new image, color space, reference file, or color matrix setting). The Display input(or Corrected) dropdown menu, immediately to its left, is enabled. You can choose one of two selections.
| Display input | Color differences (input − ideal) are shown in most displays, and [Input − ideal] Color differences are shown in the text in the lower left. Two displays are unaffected by this setting: Pseudocolor color difference and Split colors, where (corrected − ideal) is shown on the bottom. |
| Display corrected | Color differences (corrected − ideal) are shown in most displays, and [Corrected − ideal] Color differences are shown in the text in the lower left. |
The EXIF data and Color matrix display has a summary of results.
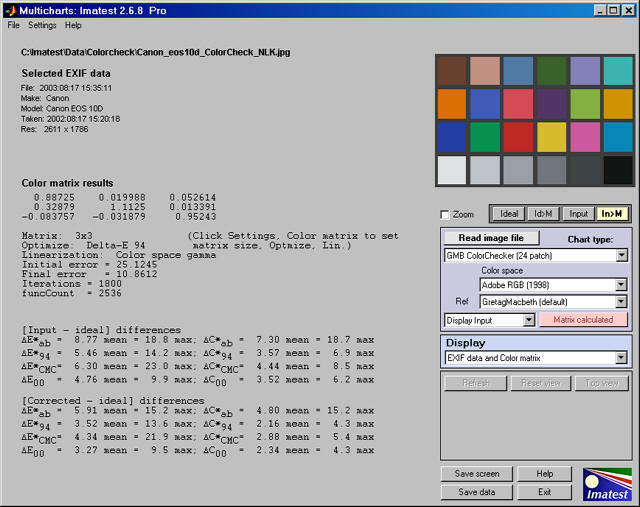
Exif and Color matrix view
The color correct matrix, results summary, and both [input - ideal] and [corrected -ideal] color difference summaries are shown. The initial and final error numbers shows how much the selected metric (in this case the sum of squares of Delta-E 94 for all patches with L*>10 and L*<95)>